讓理科生也無法反駁的計算《遠距離的聚會方式》畫條直線就能搞定啦~

圖片來自:https://www.instiz.net
身邊有沒有一兩位住的特~別~遠的朋友呢?跟這些朋友聚會總要約個中間點碰面才行,雖然可以遷就某人到離他比較近的地方但會讓另外幾位朋友累死就是了(笑)。之前在推特上有位推友跟大家分享如何與住很遠的朋友"公平"碰面,這個「方法」非常公正,完美到理科生都無法反駁,而這個「遠距離的聚會方式」也意外爆紅,讓大家瘋狂tag身邊朋友要來算算彼此的"中間點"在哪裡?
原汁原味的內容在這裡如果今天想跟另外兩位朋友碰面,但三人居住地都離彼此很遠怎麼辦?
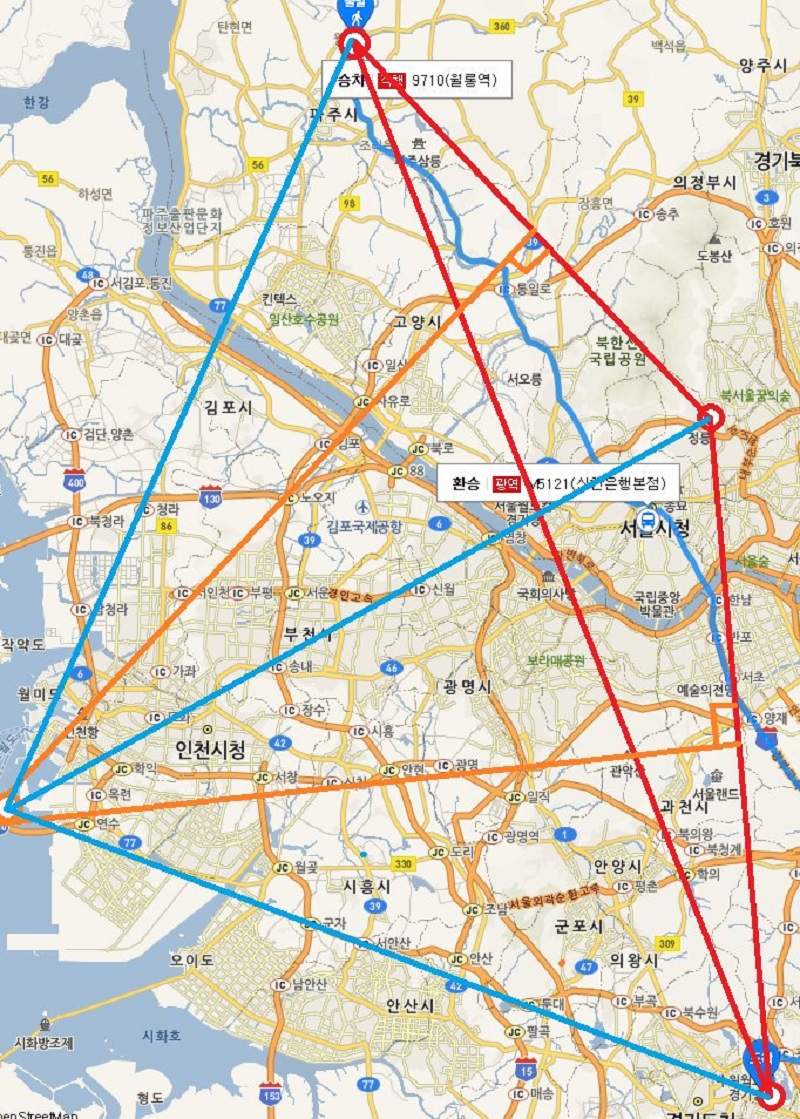
住在三個不同地方的朋友要決定碰面地點,有一個人用不偷懶的邏輯計算方式,把下次要見面的地點訂為直線距離最公平的仁川海邊。
서로 다른 세 곳에 사는 친구들과 어디서 만날지 정한 결과 한 명이 꿀빨 수 없다는 논리에 의해 다음 모임 장소는 모두 직선 이동거리가 공평한 인천앞바다로 정해졌다. pic.twitter.com/75Kfc9gSl1
— Pvt.Martin (@zhfdhqm) 2018年7月15日
簡單來說就是透過直線計算方式算出對三個出發地來說都是等同距離的地方,而直線交錯點就是最「公平」的集合地,因為這地方對誰來說都是一樣的距離w
圖片來自:https://twitter.com/zhfdhqm
在這串推文下還有補充把此方法給另外兩位朋友看的結果
雖然是用手畫的可能有些微誤差,但這樣已經足夠了。三個人中有兩個是理科生,對此無法反駁w
손그림이라 어느정도의 오차가 있을 수 있지만 이정도면 모두 만족할 수 있음. 세 명 중 두 명이 이과생이니까 반박 불가
— Pvt.Martin (@zhfdhqm) 2018年7月15日
理科生表示:嗯~這個集合地我找不出任何吐槽點(欸)

圖片來自:https://www.instiz.net
隨堂測驗:一位朋友住在石門、一位朋友住在花蓮、一位朋友住在屏東,請問這三人的直線距離集合地是?
部分資料來自網路 ( Twitter )