誰說數學沒有用《Pokemon Go尋寶法》有理由勸孩子好好讀書了……

圖片來自：http://pokemongo-master.com

大家唸書的時候有沒有想過「幹嘛要學這種以後用不到的科目呢？」，其實每一個科目、每一個理論說不定都會在意想不到的時候派上用場！最近有位日本網友教導大家將簡單的數學幾何套用在《Pokemon Go》能夠有效提升捕捉寶可夢的效率，如此一來就有理由勸孩子好好讀書了吧……

「弦的中垂線必通過圓心」

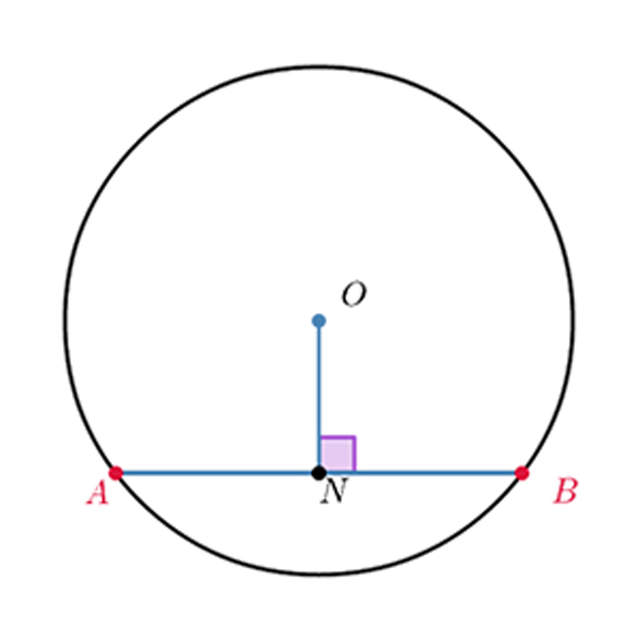
圖片來自：http://hanluninfo.dyndns.org:5050

差不多在國中的數學科目就教過圓上任一弦的中垂線（垂直平分線）必通過圓心，大家雖然學過這個定理但是曾經應用在現實生活嗎？對於《Pokemon Go》的玩家而言終於有機會實踐了……

使用雷達尋找寶可夢！

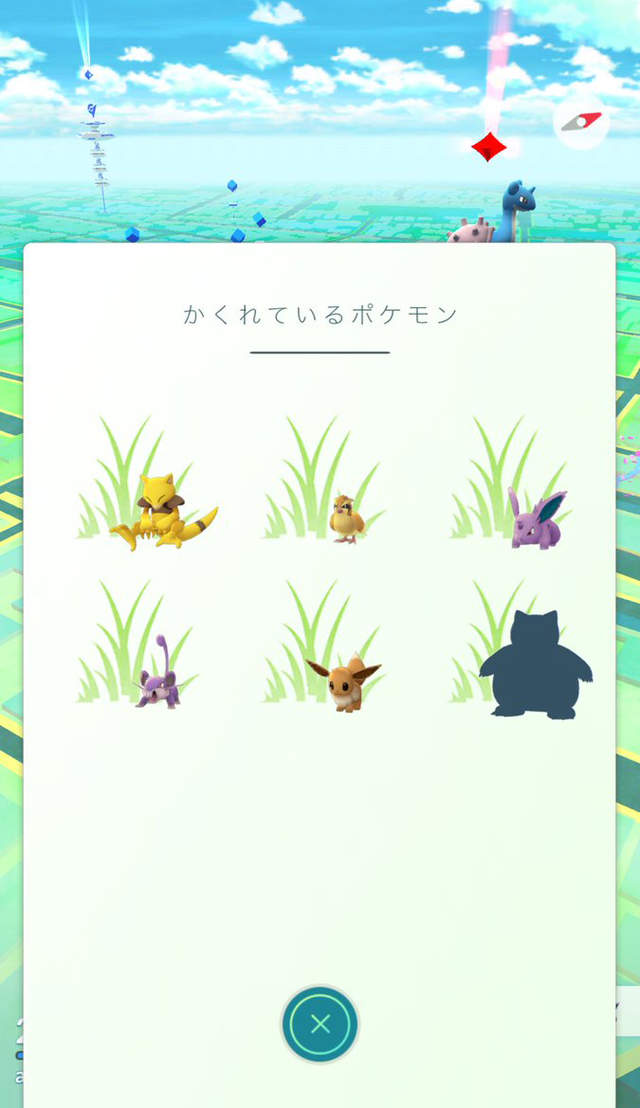
圖片來自：https://twitter.com/astro_waste

《Pokemon Go》的雷達會顯示玩家周圍的寶可夢，沒捕捉過的則只會看到影子輪廓，由於雷達是偵測一個圓型範圍而沒有顯示方位因此不容易立刻判斷寶可夢的位置，日本網友MAEDA Katsuyuki就將運用幾何定理的尋寶法做成一張圖解引發熱烈討論！

如何使用幾何定裡尋寶的圖解

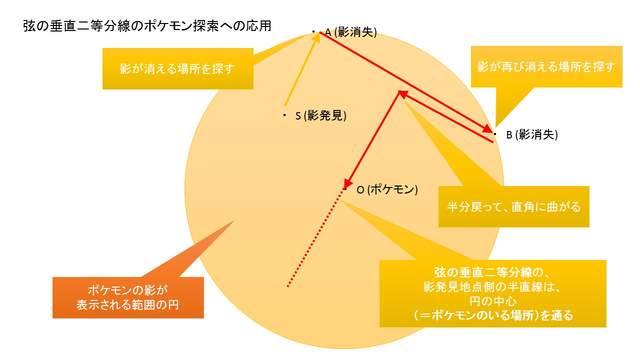
圖片來自：https://twitter.com/keikuma

以下就一個一個步驟解說吧……

尋找寶可夢的蹤跡在哪裡消失！

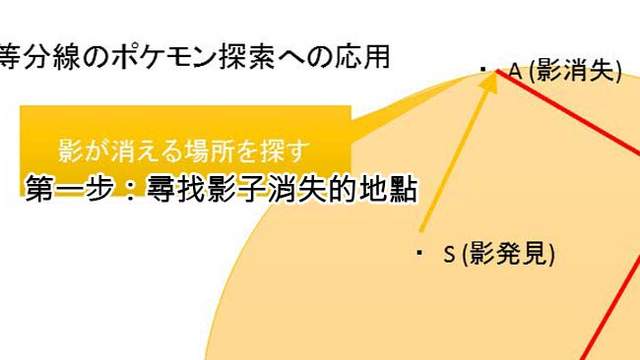
圖片來自：https://twitter.com/keikuma

假設玩家一開始在S點發現寶可夢的蹤跡，首先就要趕緊找到影子消失的地點A，這個時候就可以確定A點位在寶可夢被雷達偵測的圓形範圍邊緣，也就是圓周之上了！

尋找第二個消失的地點！

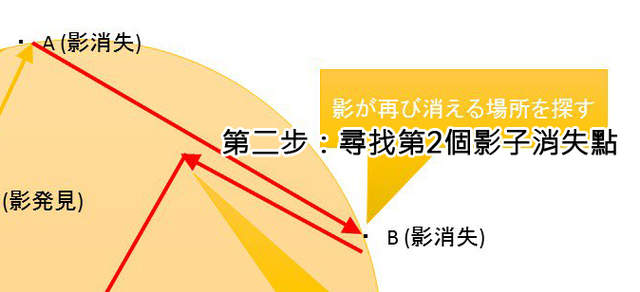
圖片來自：https://twitter.com/keikuma

找到A點以後，接著轉彎再次進入雷達偵測的範圍之內，然後直直走到下一個影子消失的地點B，這個AB連線就是以寶可夢為中心的圓形上的一條弦了！

回頭尋找中垂線路徑！

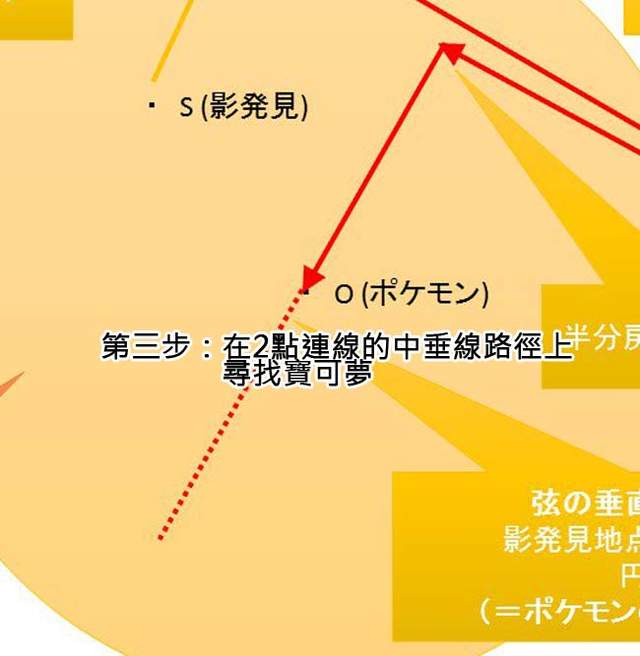
圖片來自：https://twitter.com/keikuma

最後就是從B點回頭走到AB連線的中點，沿著通過這一點並且與AB連線垂直的路徑尋找就可以發現寶可夢了！當然目標也可能會在圖示的另外一側，玩家要是發現沿著中垂線走著走著影子竟然消失就是走反囉！

運用簡單的幾何數學成功找到寶可夢！

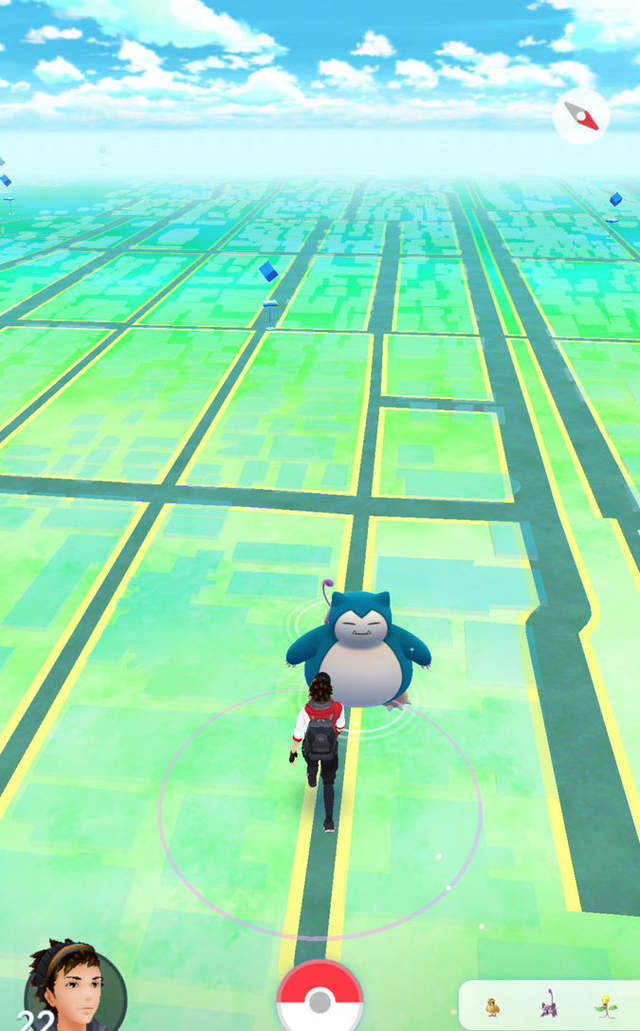
圖片來自：https://twitter.com/astro_waste

常常聽人家說「幹嘛要學這種以後用不到的科目呢？」，從這個案例可以了解學會的知識永遠不知道會在什麼時候突然派上用場啊！

對於小學都沒畢業的10歲少年來說可能困難了一點！？

圖片來自：http://vedifisub.blogspot.tw

（ﾟ∀ ﾟ）這樣就有理由叫小孩子好好讀書啦！

遊戲,神奇寶貝,Twitter,推特,教學,Android遊戲,IOS遊戲,精靈寶可夢,Pokémon-GO